黃金比例,或被稱為黃金分割率,在藝術領域上一向是很專業的知識,許多藝術家或攝影師將其視為一張美麗作品的必要元素,而能夠從現實世界中看出被自然界隱藏起來的黃金比例的能力,也被世人稱為擁有攝影眼的神奇技巧。但是你知道一張照片上的哪一個位置,是符合美麗影像的黃金比例嗎?
因為我這個人沒唸過什麼書,對攝影理論也是一知半解,所以我的作品其實就是自己隨便亂拍一通的照片。
不過,幾天前竟然有個女生跑來問不才在下我:「什麼是攝影的黃金比例?」
我很想惡狠狠的回他:「去問神奇海螺辣。」
但是為了怕被海K一頓,所以我在背完維基百科之餘,乾脆在這篇文章中替大家簡單整理一下,關於攝影黃金比例的相關學理與應用。
大樓梯是提示。
想要探討影像的黃金比例(Golden Ratio),我們必須先瞭解一件事情,既然我們在談的是一種比例,表示有數學家將這個美感上的現象,透過數學與數字,呈現在世人眼前。(不過我的數學一向不好,尤其是代數,幾何倒是還不錯,大約是天地之差這樣 =w=)。
嚴格來說,黃金比例只是一種數字化後的「美之典範」,卻沒有「絕對之美」的內涵。
因此,「某個天才科學家或數學家,在某天的午後,突然靈光一現的設計出一套數學式,並且立馬要求大家認同這個比例就是黃金比例。」─── 這種事不可能發生的。
美是一種主觀,必然包含情緒、情感等意識在其中,而那是極為私密的自我。
對我而言,我喜歡的照片就是看了之後能夠獲得感動的作品。
因此,黃金比例雖然可以提供攝影初學者一個遵循的構圖方向,但卻必須時時刻刻提醒自己,構圖與情感交織的藝術才是更重要的。
費氏數列
說來奇妙,黃金比例原本是數學家們透過觀察自然界眾多的美麗構圖後,用數字與幾何學建構出的一門新理論。
但是在費氏數列(Fibonacci Sequence,費波那西數列)的遞歸計算中,最後被推導出來的結果,竟然在形構上與大自然界許多生物的結構相雷同。因此才有人常將黃金比例與費氏數列混成一談。
費氏數列的公式為:「a1=a2=1,a(n+2)=a(n+1)+a(n)」。
逐一代入數字計算,便會依序產生成一無限長串數列:「1,1,2,3,5,8,13,21,34,55,89,144,233,377,……」。
如果我們將前項除以後項,便能得到一組數值,這組數值便是所謂的黃金比例。並且隨著進行除法的數字越大,會越趨近:
- 55/34=1.617647
- 89/55=1.618181
- 144/89=1.617977
- 233/144=1.618055
黃金切割率

黃金分割是根據黃金比例,將一條線分割成兩段。總長度 a + b 與長度較長的 a 之比等於 a 與長度較短的 b 之比。
黃金切割率,又稱黃金比,是一種數學上的比例關係。
黃金分割具有嚴格的比例性、藝術性、和諧性,蘊藏著豐富的美學價值。應用時一般取 0.618 或 1.618 ,就像圓周率在應用時取3.14一樣。黃金分割早存在於大自然中,呈現於不少動物和植物外觀。現今很多工業產品、電子產品、建築物或藝術品均普遍應用黃金分割,呈現其功能性與美觀性。
常用希臘字母  表示黃金比值,用代數式表達就是:
表示黃金比值,用代數式表達就是: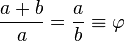
下面是一張我設計的觀景窗示意圖。示意圖中間的雙橫線、雙垂線以及四線交點,是模擬單眼相機的觀景窗畫面,或在其他數位相機 LCD 螢幕可透過設定進行呈現的資訊。
在上圖中,我設定垂直軸各點為代號 A 到 M,而水平軸各點為代號 A’ 到 S’ ,並以垂直與水平之間的交點,代表畫面上不同的座標點。
在習慣上,當我們進行構圖時,所謂的黃金比例此時會落在主線上,即 E、I、G’ 及 M’等四線段上,依照拍攝內容來決定該使用哪一條線段。
另外,如果影像有主題的話,依據黃金比例,我們通常會擺設在 EG’、IG’、EM’ 及 IM’ 四個交點上。
以上圖景觀窗內的大 Q 來看,視覺上的主交點會落在 IM’ 交點上,也就是 Q 的斜線上。你是否也是這樣覺得呢?





發佈留言